:九年级第一学期数学切线与几何计算辅助线教案

切线与几何计算辅助线

一、本节重点讲解圆的切线的性质与判定方法，以及与切线相关的圆中的几何计算问题。

切线辅助线：①有交点，连半径，证垂直；②无交点，作垂直，证半径。

二、典例精析

知识点：切线与几何计算

【例1】已知，如图，在△ADC中，∠ADC=90，以DC为直径作半圆O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED=2∠C。

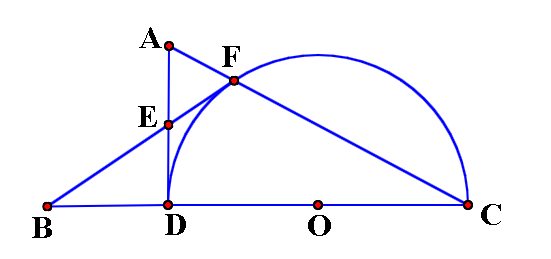
(1)求证：BF是O的切线；

(2)若BF=FC，AE=，求O的半径。

思路分析：

第一问：切线的证明常考题目，一般有这样的规律：①有交点，连半径，证垂直；②无交点，作垂直，证半径（即证明到直线的垂直线段就是半径） 。本题是第①

种情况。

第二问：由于BF=FC，这说明是等腰三角形，等腰则底角相等，这是我们推导的起点。

思路探究：

(1) 连接半径OF，由于圆的半径相等得等腰三角形，则底角相等，然后传递角的关系到外角。

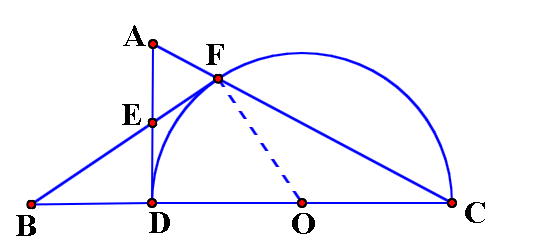
证明：连接辅助线OF，

(2)这是一个包含了特殊角的直角三角形。我们需要利用这点，通过已知的AE计算直径DC，首先得到角度条件，结合AE来解。

方法总结：

第一问：移动点A，再次体验这一推导过程，体会有交点，连半径，证垂直。

第二问：能够利用切线长定理中线段相等的关系是本题的关键。同时，从条件到目标的计算过程中，各种等腰三角形、等边三角形、特殊直角三角形的识别和构造也起了重要的作用。