1.(2019安徽)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=2PC;
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.

证明:(1)∠ACB=90°,AB=BC,
∴∠ABC=45°=∠PBA+∠PBC,
又∠APB=135°,
∴∠PAB+∠PBA=45°,
∴∠PBC=∠PAB,
又∠APB=∠BPC=135°,
∴△PAB∽△PBC.
(2)△PAB∽△PBC,
∴ ,
,
在Rt△ABC中,AB=AC,
∴ ,
,
∴ ,
,
∴PA=2PC.
(3)如图,过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,

∴PF=h1,PD=h2,PE=h3,
∠CPB+∠APB=135°+135°=270°,
∴∠APC=90°,
∴∠EAP+∠ACP=90°,
又∠ACB=∠ACP+∠PCD=90°,
∴∠EAP=∠PCD,
∴Rt△AEP∽Rt△CDP,
∴ ,即
,即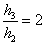 ,
,
∴h3=2h2,
△PAB∽△PBC,
∴ ,
,
∴ ,
,
∴ .
.
即:h12=h2·h3.
文档为doc格式
版权声明:以上文章中所选用的图片及文字来源于网络以及用户投稿,由于未联系到知识产权人或未发现有关知识产权的登记,如有知识产权人并不愿意我们使用,如果有侵权请立即联系:1234567890@qq.com,我们立即下架或删除。
相关文章:
附近文章:
快读网 www.kuaidu.com.cn 网站邮箱:wodd7@hotmail.com